Stéphan Bourget, enseignant de physique, Cégep Vanier
Elisabeth Guérard, AESTQ

Kassandra L’Heureux, étudiante au doctorat, Université de Sherbrooke et Valérie Vinuesa, professionnelle de recherche Chaire de recherche pour l’éducation en plein air, Université de Sherbrooke


Phylippe Laurendeau, GRICS | Rédacteur en chef de la revue Spectre


Les étudiants et étudiantes du collégial arrivent souvent à leurs premiers cours de physique avec des idées préconçues contradictoires qui nuisent à leur compréhension. Halloun et Hestenes (1985) rapportent que les croyances (généralement erronées) des étudiants sont très stables et conduisent à une mauvaise interprétation systématique du matériel des cours d’introduction. Pour améliorer l’apprentissage et offrir une expérience plus authentique, il vaut la peine d’examiner la construction des connaissances scientifiques et comment elle peut éclairer l’enseignement des sciences. L’enseignement par modélisation, qui sera présentée dans ce qui suit, est une méthode d’enseignement qui peut s’avérer efficace pour y arriver.
Les connaissances scientifiques sont organisées en théories et modèles servant à interpréter et à donner du sens aux données empiriques (Hestenes, 1987). En physique, nous utilisons des modèles schématiques, graphiques et mathématiques pour décrire, expliquer ou prédire des phénomènes. L’enseignement par modélisation a pour principe de reproduire le processus de construction de tels modèles et est donc fortement enraciné dans l’approche expérimentale. C’est à partir des expériences de laboratoire que la théorie est développée, et non l’inverse. Ainsi, les étudiants et étudiantes commencent un cycle d’apprentissage par l’investigation expérimentale d’un phénomène, avant même d’avoir appris quoi que ce soit de manière théorique à son sujet.
Pour illustrer l’idée générale, considérons ce qui pourrait arriver en étudiant la réfraction d’un faisceau lumineux monochromatique à travers un prisme de verre. Les observations pourraient d’abord mener à une analogie physique avec un camion-jouet motorisé (analogue à la lumière) se déplaçant à vitesse constante et passant d’une surface en béton (analogue à l’air) à une surface couverte de boue (analogue au verre), où le déplacement est plus ardu. Cela pourrait à son tour inspirer quelques expériences conduisant à une expression mathématique de la loi de la réfraction. Ces deux modèles pourraient ensuite être combinés dans un modèle conceptuel de rayons lumineux se déplaçant en lignes droites à une vitesse constante jusqu’à ce qu’ils atteignent la limite d’un milieu où la lumière se déplace à une vitesse inférieure. À cette limite, les rayons lumineux transmis se comportent comme la loi de la réfraction décrit.
Par ailleurs, une autre analogie physique aurait pu être conçue, comme une sauveteuse (analogue à la lumière) courant pour sauver un nageur en détresse dans les plus brefs délais. Le chemin optimal, du sable (analogue à l’air) à l’eau (analogue au verre) correspondrait à la loi de la réfraction. Combiné au modèle empirique, cela pourrait conduire à un développement ultérieur du modèle conceptuel en incorporant le principe de moindre temps de Fermat.
C’est ce genre de modélisation conceptuelle à partir de l’expérience de laboratoire qui constitue en quelque sorte une des bases de l’enseignement par modélisation. Les modèles se complexifient graduellement, sont généralisés, puis déployés à d’autres phénomènes jusqu’au moment où ils sont pris en défaut et exigent leur amélioration ou leur remplacement par des modèles plus robustes.
L’enseignement par modélisation est une méthode d’enseignement des sciences où l’accent est mis sur l’enquête, l’observation, la collaboration, la communication et le raisonnement, avec un enseignant agissant comme questionneur plutôt que comme fournisseur de connaissances (Megowan, 2010). Il a été développé par les physiciens et Hestenes (1987) à l’Université d’État de l’Arizona et adapté au secondaire (américain) par Wells et ses collaborateurs (1995).
L’enseignement par modélisation suit un cycle qui est répété plusieurs fois. Megowan (2010) l’a divisé en trois phases : la construction du modèle, les essais et l’élaboration du modèle, puis l’application du modèle. Dans la première phase, un laboratoire paradigmatique aide les étudiants et étudiantes à identifier collaborativement un modèle et ses paramètres (la première section illustrait une possible approche dans l’étude de la réfraction). Ce laboratoire génère des conversations qui les amènent à organiser ce qu’ils savent et ce qu’ils veulent savoir, à générer des hypothèses testables, à chercher des preuves et à construire un argumentaire. Cela se termine par une « réunion de conseil », une sorte de plénière entre les équipes. Dans la deuxième phase, le modèle est affiné et testé à travers une variété de tâches et de problèmes qui suscitent une meilleure maitrise du modèle initialement identifié. Dans la troisième phase, les équipes utilisent le modèle pour résoudre des problèmes plus complexes et contextualisés. Un laboratoire pratique et une évaluation de fin d’unité complètent le processus. Megowan (2010) recommande de former des groupes de trois personnes pour le travail collaboratif précédant les réunions de conseil essentiellement dirigées de manière autonome par les étudiants et étudiantes.
Le cycle est répété lorsque les investigations mettent au jour des phénomènes pour lesquels les modèles existants sont insuffisants, voire inappropriés. Par exemple, l’étude d’un charriot roulant sur un plan incliné mettra en défaut le modèle cinématique du mouvement à vitesse constante. Selon l’orientation choisie, l’étude du rebond d’une balle au sol montrera les limites du modèle cinématique du mouvement uniformément accéléré et pourrait être l’occasion de présenter l’idée d’énergie pour arriver à un modèle causal de celui-ci, ou peut-être préfèrera-t-on simplement considérer l’insuffisance des modèles cinématiques (descriptifs) à expliquer le mouvement, justifiant un nouveau cycle pour développer un modèle causal avec la notion de force. Un autre modélisateur pourrait par ailleurs préférer montrer l’insuffisance du modèle de mouvement uniformément accéléré pour décrire les collisions, et ainsi entamer un nouveau cycle qui développera la notion de quantité de mouvement.
Desbien (2002) a décrit sept éléments d’une bonne gestion du discours en modélisation :
Le sixième point, surtout sa seconde partie, est discutable. Plusieurs modélisateurs, surtout au secondaire, préfèreront offrir plus d’encadrement. Même au collégial, cet encadrement additionnel est souvent nécessaire pour guider (et sécuriser) le groupe. L’idéal demeure néanmoins de s’effacer autant que possible et de manière progressive pour que les étudiants prennent la responsabilité du processus. Hestenes (1997) précise d’ailleurs que l’enseignant ou l’enseignante doit guider l’investigation et la discussion avec des questions et des remarques socratiques. Il ajoute que les termes techniques et les outils de représentation sont présentés par l’enseignant, car ils sont nécessaires pour affiner les modèles, faciliter les activités de modélisation et améliorer la qualité du discours.
Lorsqu’ils sont adaptés à des situations spécifiques, les modèles généraux deviennent spécifiés et peuvent être utilisés pour résoudre des problèmes spécifiques. Des outils de modélisation couramment utilisés en mécanique sont les cartes de mouvement, les graphes cinématiques, les schémas de système, les diagrammes de forces ou de corps libres, et les graphiques à secteurs ou à barres d’énergie (figures 1 et 2). Il en existe d’autres et si le temps le permettait, il serait même possible de développer des simulations avec Excel, Python, Mathematica ou des logiciels de dynamique des systèmes comme Vensim ou Powersim Studio (l’auteur a utilisé Pyret en classe de mise à niveau). Ces outils sont des représentations de différents aspects d’un phénomène et leur multiplicité renforce un modèle tout en permettant une compréhension plus approfondie qui peut être vérifiée par leur cohérence.
Figure 1. Exemples de représentations en enseignement par modélisation. Ce diagramme LOL inclut un schéma situationnel, des graphiques à barres d’énergie avec représentation du flux d’énergie à travers le système choisi, et l’équation correspondante. Il est abordé lors de la discussion des concepts de réservoirs (à l’intérieur d’un système) et de transferts (vers l’intérieur ou l’extérieur d’un système) d’énergie, ainsi que de sa conservation.
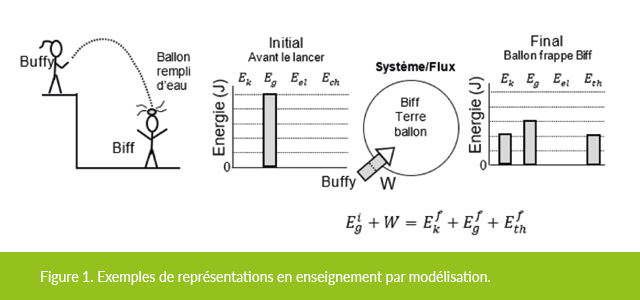
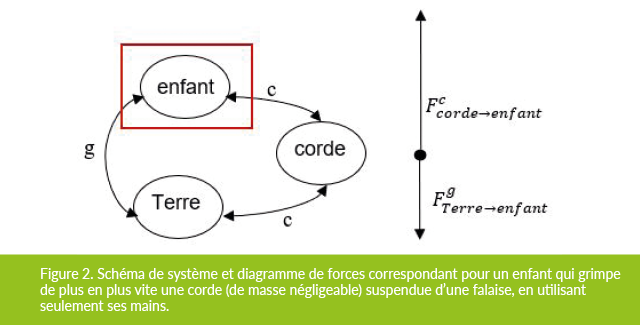
Figure 2. Schéma de système et diagramme de forces correspondant pour un enfant qui grimpe de plus en plus vite une corde (de masse négligeable) suspendue d’une falaise, en utilisant seulement ses mains. Le schéma de système est un moyen de bien identifier le système d’intérêt et de prédire le nombre de forces à apparaitre dans le diagramme de forces (en comptant le nombre d’interactions avec des agents extérieurs).
L’utilisation du tableau blanc (souvent portatif) est une autre caractéristique centrale de l’enseignement par modélisation (Megowan, 2007), car il sert de médiateur du discours et permet aux raisonnements d’être extériorisés et ouverts à l’examen des pairs. C’est un moyen très efficace pour détecter les idées fausses et y remédier, mais certaines conditions doivent être remplies pour que cela réussisse.
En enseignement par modélisation, les présentations magistrales sont sinon absentes, à tout le moins réduites au strict minimum. L’essentiel du temps de classe est passé en travail d’équipe, soit en laboratoire, soit autour d’un tableau blanc à synthétiser des résultats, une réflexion ou une démarche, soit en « réunion de conseil », toute la classe idéalement assise en cercle pour présenter les tableaux blancs et échanger à leur sujet de manière à produire un consensus permettant d’avancer dans l’apprentissage.
La recherche sur l’enseignement de la physique s’appuie largement sur le Force Concept Inventory (FCI) pour évaluer les apprentissages en mécanique. Environ 7 500 élèves des États-Unis en physique du secondaire ont participé à un projet d’enseignement par modélisation en 1995-1998. Hestenes (2006) rapporte des moyennes de 29 % et 69 % avant et après le test pour les modélisateurs experts, comparativement à 26 % et 52 % pour les modélisateurs débutants, et à 26 % et 42 % pour les enseignants traditionnels. Cela correspond aux résultats recueillis entre 1994 et 2000 pour 20 000 élèves (Hestenes, 2000). Madsen, McKagan et Sayre (2015) ont également signalé des améliorations attitudinales significatives résultant d’un accent explicite sur la création de modèles et le développement de croyances plus expertes.
En 2001, l’enseignement par modélisation a été reconnu comme l’un des deux seuls programmes scientifiques exemplaires de la maternelle à la 12e année sur les 27 qui ont été évalués (U.S. Department of Education, 2001). En 2008, Brewe rapportait que 10 % des enseignants et enseignantes de physique du secondaire, aux États-Unis, ont reçu une formation formelle sur la méthode d’enseignement par modélisation.
La modélisation est également utilisée dans des universités et collèges américains. Malgré des résultats positifs, des obstacles ralentissent son adoption généralisée dans l’enseignement supérieur. La modélisation est mieux mise en œuvre à l’aide d’une approche pratique qui s’adapte bien aux locaux qui combinent théorie et laboratoire en tout temps, et elle peut nécessiter une couverture de contenu réduite. De plus, il existe actuellement un manque de ressources de niveau universitaire, sans compter que la plupart des manuels ignorent le rôle des modèles et omettent souvent une utilisation étendue des représentations (Brewe, 2008). Les modélisateurs, incluant l’auteur, arrivent cependant à relever ces défis pour permettre à leurs étudiants et étudiantes de développer une compréhension plus juste de la pratique scientifique et de ses modèles théoriques.
L’enseignement par modélisation est une approche fort prometteuse pour favoriser l’apprentissage plus authentique des sciences comme la physique. Malgré les contraintes (celle de ne pas pouvoir être au laboratoire en tout temps, forçant ainsi un rythme plus ou moins naturel, étant la plus importante), l’auteur a réussi à utiliser l’approche pour enseigner la mécanique au collégial, et cela sans réduire le matériel requis pour l’examen final commun. La performance était satisfaisante pour une mise en œuvre débutante (pour les détails, voir Bourget, 2020). Avec expertise et pratique, et avec l’optimisation en cours de la séquence d’enseignement, il s’attend à ce que des résultats d’apprentissage plus élevés soient obtenus et il encourage sans hésiter toutes les personnes qui ont envie de renouveler leur enseignement à considérer sérieusement cette approche.
Bourget, S. (2020). Learning outcomes of modelling vs. Regular instruction in a CEGEP introductory physics course. Université Sherbrooke.
Brewe, E. (2008). Modeling theory applied: Modeling instruction in introductory physics. American Journal of Physics, 76(12), 1155.
Desbien, D. M. (2002, 1er janvier). Modeling discourse management compared to other classroom management styles in university physics. ProQuest Dissertations Publishing.
Halloun, I. A. et Hestenes, D. (1985). Common sense concepts about motion. American Journal of Physics, 53(11), 1056-1065.
Halloun, I. A. et Hestenes, D. (1987). Modeling instruction in mechanics. American Journal of Physics, 55, 455-462.
Hestenes, D. (1987). Toward a modeling theory of physics instruction. American Journal of Physics, 55(5), 440-454.
Hestenes, D. (1997). Modeling methodology for physics teachers. AIP Conference Proceedings, 399, 935-958.
Hestenes, D. (2000). Findings of the modeling workshop project, 1994 - 2000. Une section d’un rapport NSF final.
Hestenes, D. (2006). Notes for a modeling theory. In Proceedings of the 2006 GIREP conference: Modeling in physics and physics education (Vol. 31).
Madsen, A., McKagan, S. B. et Sayre, E. C. (2015). How physics instruction impacts students’ beliefs about learning physics: A meta-analysis of 24 studies. Physical Review Special Topics - Physics Education Research, 11(1).
Megowan, M. C. (2007). Framing discourse for optimal learning in science and mathematics. Arizona State University.
Megowan, M. C. (2010). The modeling method of instruction in physics: How to do it! Proceedings of the 2010 Chinese Association of Physics Education and Research Conference.
U.S. Department of Education, Office of Educational Research and Improvement (2001). Exemplary and promising science programs, 2001. Washington, DC.
Wells, M., Hestenes, D. et Swackhamer, G. (1995). A modeling method for high school physics instruction. American Journal of Physics, 63(7), 606-619.